Assumptions of Neoclassical Economics ("Homo Economicus")
• Selfishness - an individual chooses on the basis of his/her own interests (no true, systematic altruism)• Stable, exogenous preferences - what the individual wants is well-defined, available to introspection, and stable over time
• Formal rationality - an individual's preferences, tastes, etc. are consistent with each other
Rational Choice Theories for Individuals
- Utility theory one agent, choice depends only on states of nature
- Utility theory one agent, choice depends only on states of nature
Example: A decision that depends on states of nature
• Options:
- Plan picnic outdoors
- Plan picnic indoors
• Options:
- Plan picnic outdoors
- Plan picnic indoors
• Possible states of nature
- Rain
- No rain
- Rain
- No rain
• Choice depends on likelihood of rain, relative quality of picnic indoors/outdoors with and without rain
Rational Choice Theories for Individuals (Von Neumann and Morgenstern, 1944)
- Utility theory one agent, choice depends only on states of nature
- Game theory more than one agent, choice depends on what other agents may choose
Example: a decision that depends on what others may do
• Options:
- Go to the beach
- Go to the cinema
• Your friend may choose to:
- Go to the beach
- Go to the cinema
• You cannot control or know what your friend will do
• Both of you know each other's preferences
• Choice depends on what you think your friend will do, which depends on what s/he thinks you will do, and so on...
Expected Utility Theory - Crucial Features
Utility ("degree of liking") is defined by (revealed) preferences
- i.e. U(A) > U(B) iff A is preferred to (chosen over) B
Expected Utility Theory - Crucial Features
Utility ("degree of liking") is defined by (revealed) preferences
- i.e. U(A) > U(B) iff A is preferred to (chosen over) B • Preferences are well ordered
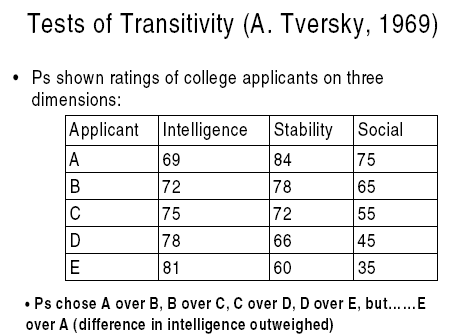
- i.e. transitive: If A ? B and B ? C, then A ? C
Utility ("degree of liking") is defined by (revealed) preferences
- i.e. U(A) > U(B) iff A is preferred to (chosen over) B
Preferences are well ordered
- i.e. transitive: If A ? B and B ? C, then A ? C
Choices under uncertainty are determined by expected utility
- Expected utility is a probability-weighted combination of the utilities of all n possible outcomes O,
ΣU(O)P(O)
Example:
Application of Utility Theory
• Options:
- Gamble (50% chance to win $100; else $0)
- Sure Thing (100% chance to win $50)
• Expected values are the same:
- EV(Gamble) (.5) ($100) + (.5) ($0) = $50
- EV(Sure Thing) (1) ($50) = $50
• But their expected utilities may still differ
- EU (Gamble) = .5U ($100) + .5U ($0)
- EU (Sure Thing) = U($50)
Expected utility theory says that utilities are...
- Not directly observable (internal to an individual)
- Not comparable across individuals
- Constrained by revealed preferences (i.e. choices between gambles)
• Note: Anderson gets the relationship between utility and value wrong
Do people's choices obey the theory of expected utility (i.e., formal rationality)?
Expected Utility Theory - Crucial Features
• Utility ("degree of liking") is defined by
(revealed) preferences
- i.e. U(A) > U(B) iff A is preferred to (chosen over) B
Utility versus Preference (Lichtenstein and Slovic, 1971; 1973)
• Ps given two options:
- P bet: 29/36 probability to win $2
- $ bet: 7/36 probability to win $9
• Two conditions:
- Choose one: Most prefer P bet
- Value the bets: Most value $ bet higher
• Shows utility (based on cash value) is not consistent with revealed preference
Expected Utility Theory - Crucial Features
• Utility ("degree of liking") is defined by
(revealed) preferences
- i.e. U(A) > U(B) iff A is preferred to (chosen over) B
- Contradicted by preference reversal
Expected Utility Theory - Crucial Features
• Utility ("degree of liking") is defined by
(revealed) preferences
- i.e. U(A)> U(B) iff A is preferred to (chosen over) B
- Contradicted by preference reversal
• Preferences are well ordered
- i.e. transitive: If A ? B and B ? C, then A ? C
Expected Utility Theory - Crucial Features
• Utility ("degree of liking") is defined by (revealed) preferences
- i.e. U(A)> U(B) iff A is preferred to (chosen over) B
- Contradicted by preference reversal
• Preferences are well ordered
- i.e. transitive: If A ? B and B ? C, then A ? C
- Contradicted by three-option intransitivities (and preference reversals)
Expected Utility Theory - Crucial Features
• Utility ("degree of liking") is defined by (revealed) preferences
- i.e. U(A) > U(B) iff A is preferred to (chosen over) B
- Contradicted by preference reversals
• Preferences are well ordered
- i.e. transitive: If A ? B and B ? C, then A ? C
- Contradicted by three-option intransitivities (and preference reversals)
• Choices under uncertainty are determined by expected utility
- Expected utility is a probability-weighted combination of the utilities of all in possible outcomes 0,
• Choose between
- A. Sure win of $30
- B. 80% chance to win $45
Testing Expected Utility (Tversky and Kahneman, 1981)
• Choose between:
- A. Sure win of $30
- B. 80% chance to win $45 • Choose between:
- C. 25% chance to win $30
- D. 20% chance to win $45
Testing Expected Utility (Tversky and Kahneman, 1981)
• Choose between:
- A. Sure win of $30 [78 percent]
- B. 80% chance to win $45 [22 percent]
• Choose between:
- C. 25% chance to win $30 [42 percent]
- D. 20% chance to win $45 [58 percent]
Testing Expected Utility (Tversky and Kahneman, 1981)
• Choose between:
- A. Sure win of $30 [78 percent]
- B. 80% chance to win $45 [22 percent] • Choose between:
- C. 25% chance to win $30 [42 percent] - D. 20% chance to win $45 [58 percent]
But this pattern is inconsistent with EUT:
- EU(A)>EU (B) => u($30)>.8u($45)
- EU(D)>EU(C) => .25u($30) <.2u($45)
- Multiply both sides of bottom inequality by 4: contradicts top inequality
Testing Expected Utility (Tversky and Kahneman, 1981)
• Choose between:
- A. Sure win of $30 [78 percent]
- B. 80% chance to win $45 [22 percent]
Choose between:
- C. 25% chance to win $30 [42 percent]
- D. 20% chance to win $45 [58 percent]
But this pattern is inconsistent with EUT:
- EU(A)>EU (B) => u($30)>.8u($45)
- EU(D)>EU(C) => .25u($30) <.2u($45)
- Multiply both sides of bottom inequality by 4: contradicts top inequality
• This is called a "certainty effect": certain gains have extra psychological value
Expected Utility Theory - Crucial Features
• Utility ("degree of liking") is defined by (revealed) preferences
- i.e. U(A) > U(B) iff A is preferred to (chosen over) B
- Contradicted by preference reversals
• Preferences are well ordered
- i.e. transitive: If A ? B and B ? C, then A ? C
- Contradicted by three-option intransitivities (and preference reversals)
• Choices under uncertainty are determined by expected utility
- Expected utility is a probability-weighted combination of the utilities of all 'n possible outcomes O,
- Contradicted by certainty effect
So, people's choices do not obey formal rationality.
Are their preferences nonetheless stable?
Neoclassical Assumptions About Preferences
• The chosen option in a decision problem should remain the same even if the surface description of the problem changes (descriptive invariance)
A Test of Descriptive Invariance (Tversky and Kahneman, 1981)
• Consider a two-stage game. In the first stage, there is a 75% chance to end the game without winning anything, and a 25% chance to move into the second stage. If you reach the second stage, you have a choice between
- Sure win of $30 (74%)
- 80% chance to win $45 (26%)
• Your choice must be made before the game starts, i.e. before the outcome of the first stage is known
A Test of Descriptive Invariance (continued)
• But this gamble is formally identical to a problem we saw earlier, namely:
- Choose between:
• C. 25% chance to win $30 [42 percent]
• D. 20% chance to win $45 [58 percent]
• But this gamble is formally identical to a problem we saw earlier, namely:
- Choose between:
• C. 25% chance to win $30 [42 percent]
• D. 20% chance to win $45 [58 percent]
Compare:
- Consider a two-stage game. In the first stage, there is a 75% chance to end the game without winning anything, and a 25% chance to move into the second stage. If you reach the second stage, you have a choice between
• Sure win of $30 [74 percent]
• 80% chance to win $45 [26 percent]
• But this gamble is formally identical to a problem we saw earlier, namely:
- Choose between:
C. 25% chance to win $30 [42 percent]
D. 20% chance to win $45 [58 percent]
• Compare:
Consider a two-stage game. In the first stage, there is a 75% chance to end the game without winning anything, and a 25% chance to move into the second stage. If you reach the second stage, you have a choice between
- Sure win of $30 [74 percent]
- 80% chance to win $45 [26 percent]
• A violation of descriptive invariance
• This is known as a "pseudo-certainty" effect: When a stage of the problem is presented as involving a certain gain, it carries extra weight even if getting to that stage is itself uncertain.
Framing Effects (Tversky and Kahneman, 1981)
• Problem 1: Imagine that the U.S. is preparing for the outbreak of an unusual Asian disease, which is expected to kill 600 people. Two
alternative programs to combat the disease have been proposed. Assume that the exact scientific estimate of the consequences of the programs are as follows:
- If Program A is adopted, 200 people will be saved [72 percent]
- If Program B is adopted, there is 1/3 probability that 600 people will be saved, and 2/3 probability that no people will be saved. [28 percent]
• Problem 2:
- If Program C is adopted 400 people will die [22 percent]
- If Program D is adopted there is 1/3 probability that nobody will die, and 273 probability that 600 people will die. [78 percent]
• But the programs are identical! This example also violates descriptive invariance.
• Shows reflection effect: Risk aversion in the domain of gains; risk seeking in the domain of losses
Neoclassical Assumptions About Preferences
• The chosen option in a decision problem should remain the same even if the surface description of the problem changes (descriptive invariance)- Contradicted by pseudo-certainty and framing effects• The chosen option in a decision problem should remain the same even if the surface Description of the problem changes (descriptive invariance)- Contradicted by pseudo-certainty and framing effects• The chosen option should depend only on the outcomes that will obtain after the decision is made, not on differences between those outcomes and - the status quo- what one expects- the overall magnitude of the decision
Status Quo Bias (Kahnemen, Knetsch, and Thaler, 1990)
• "Sellers" each given coffee mug, asked how much they would sell if for"Buyers" not given mug, asked how much they would pay for one• Median values:- Sellers: $7.12- Buyers: $2.87• "Sellers" each given coffee mug, asked how much they would sell if for"Buyers" not given mug, asked how much they would pay for one• Median values:- Sellers: $7.12- Buyers: $2.87• "Choosers" asked to choose between mug and cash- preferred mug if cash amount was $3.12 or lower, on average• Shows "endowment effect" - we value what we have; and "loss aversion" - we don't want to lose it
alternative programs to combat the disease have been proposed. Assume that the exact scientific estimate of the consequences of the programs are as follows:
- If Program A is adopted, 200 people will be saved [72 percent]
- If Program B is adopted, there is 1/3 probability that 600 people will be saved, and 2/3 probability that no people will be saved. [28 percent]
• Problem 2:
- If Program C is adopted 400 people will die [22 percent]
- If Program D is adopted there is 1/3 probability that nobody will die, and 273 probability that 600 people will die. [78 percent]
• But the programs are identical! This example also violates descriptive invariance.
• Shows reflection effect: Risk aversion in the domain of gains; risk seeking in the domain of losses
Neoclassical Assumptions About Preferences
• The chosen option in a decision problem should remain the same even if the surface description of the problem changes (descriptive invariance)
- Contradicted by pseudo-certainty and framing effects
• The chosen option in a decision problem should remain the same even if the surface Description of the problem changes (descriptive invariance)
- Contradicted by pseudo-certainty and framing effects
• The chosen option should depend only on the outcomes that will obtain after the decision is made, not on differences between those outcomes and
- the status quo
- what one expects
- the overall magnitude of the decision
Status Quo Bias (Kahnemen, Knetsch, and Thaler, 1990)
• "Sellers" each given coffee mug, asked how much they would sell if for
"Buyers" not given mug, asked how much they would pay for one
• Median values:
- Sellers: $7.12
- Buyers: $2.87
• "Sellers" each given coffee mug, asked how much they would sell if for
"Buyers" not given mug, asked how much they would pay for one
• Median values:
- Sellers: $7.12
- Buyers: $2.87
• "Choosers" asked to choose between mug and cash- preferred mug if cash amount was $3.12 or lower, on average
• Shows "endowment effect" - we value what we have; and "loss aversion" - we don't want to lose it




No comments:
Post a Comment